Geometrie
Vektoren
Ein Vektor \(\overrightarrow v = \left( \begin{array}{c}v_1\\v_2 \\v_3 \end{array} \right) \) beschreibt eine Verschiebung. Ein Vektor hat also immer eine Richtung und eine Länge (Betrag des Vektors).
Der Vektor, der den Punkt \(A(a_1|a_2|a_3)\) auf dem Punkt \(B(b_1|b_2|b_3)\) verschiebt wird mit \(\overrightarrow{AB} = \left( \begin{array}{c}b_1 - a_1\\b_2 - a_2 \\b_3- a_3 \end{array} \right)\) (Endpunkt - Anfangspunkt) berechnet.
Der Vektor, der den Punkt \(A(a_1|a_2|a_3)\) auf dem Punkt \(B(b_1|b_2|b_3)\) verschiebt wird mit \(\overrightarrow{AB} = \left( \begin{array}{c}b_1 - a_1\\b_2 - a_2 \\b_3- a_3 \end{array} \right)\) (Endpunkt - Anfangspunkt) berechnet.
\(-\vec v=\overrightarrow{AB} \) ist der Gegenvektor zu \(\vec v = \overrightarrow{AB} \), d.h. die Richtung der Verschiebung wird gerade umgedreht.
Der Betrag eines Vektors \(|\overrightarrow{v} | = |\overrightarrow{AB} |\) ist die Länge \(d\) des Vektors bzw. der Abstand der Punkte \(A(a_1|a_2|a_3)\), \(B(b_1|b_2|b_3)\):
\[d= \sqrt{(b_1-a_1)^2 + (b_2-a_2)^2 +(b_3-a_3)^2 }\]
Ein Einheitsvektor \(\overrightarrow{v_0} \) hat den Betrag 1. Es gilt: \[ \overrightarrow{v_0} = \frac{\overrightarrow{v} }{|\overrightarrow{v} |}\] ist der Einheitsvektor von \(\overrightarrow{v} \).
Den Mittelpunkt \(M\) einer Strecke \(\overline{AB}\) erhält man, indem man die einzelnen Koordinaten addiert und durch 2 teilt: \[M\left( \frac{a_1+b_1}{2}|\frac{a_2+b_2}{2}| \frac{a_3+b_3}{2} \right)\]
Ein Vektor ist eine Verschiebung im Raum. Zwei Vektoren sind dann gleich, wenn die Verschiebung die gleiche Richtung hat, d. h. die Vektoren sind Vielfache voneinander und der Betrag der Vektoren ist jeweils gleich.
\(\overrightarrow{AB} = \overrightarrow{CD} \), falls
- \( \overrightarrow{AB} \sim\overrightarrow{CD} \) (linear abhängig) und
- \(|\overrightarrow{AB} | =|\overrightarrow{CD} | \) (Länge ist gleich).
Der Vektor, der den Ursprung auf einen Punkt \(A\) verschiebt, heißt Ortsvektor des Punktes \(A\). Zu jedem Punkt gibt es genau einen Ortsvektor, er hat dieselben Koordinaten, wie der Punkt \(A\), der Ortsvektor wird mit \(\overrightarrow{a} \) bezeichnet.
Es gilt: \(\overrightarrow{a} = \left( \begin{array}{c}a_1\\a_2 \\a_3 \end{array} \right) \) ist der Ortsvektor \(\overrightarrow{a} = \overrightarrow{0A} \) des Punktes \(A\left(a_1|a_2 |a_3\right)\).
Wichtig: Mit Hilfe von Ortsvektoren ist es möglich, Punkte mit Vektoren zu beschreiben.
Wichtig: Mit Hilfe von Ortsvektoren ist es möglich, Punkte mit Vektoren zu beschreiben.
Das Skalarprodukt muss 0 sein.
Zwei Vektoren sind genau dann orthogonal, falls das Skalarprodukt 0 ist: $$\overrightarrow a \perp \overrightarrow b \Longleftrightarrow a_1 \cdot b_1 + a_2 \cdot b_2 + a_3 \cdot b_3 = 0. $$
Zwei Vektoren sind genau dann orthogonal, falls das Skalarprodukt 0 ist: $$\overrightarrow a \perp \overrightarrow b \Longleftrightarrow a_1 \cdot b_1 + a_2 \cdot b_2 + a_3 \cdot b_3 = 0. $$
Kreuzprodukt (Vektorprodukt)
Die Vektoren \(\vec a\) und \(\vec b\) spannen eine Ebene auf, \( \vec n = \vec a \times \vec b \) steht senkrecht auf dieser Ebene.
Berechnen kann man dies auch mit Hilfe des Skalarproduktes. Wegen \[ \vec a \cdot \vec n =0 \qquad \hbox{und}\qquad \vec b \cdot \vec n =0\] erhält man \(\vec n\) als Lösung des LGS: \[\begin{align} a_1\cdot n_1 + a_2\cdot n_2 + a_3 \cdot n_3 =& \, 0\\ b_1\cdot n_1 + b_2\cdot n_2 + b_3 \cdot n_3 =& \, 0\\ \end{align}\]
Die Vektoren \(\vec a\) und \(\vec b\) spannen eine Ebene auf, \( \vec n = \vec a \times \vec b \) steht senkrecht auf dieser Ebene.
Berechnen kann man dies auch mit Hilfe des Skalarproduktes. Wegen \[ \vec a \cdot \vec n =0 \qquad \hbox{und}\qquad \vec b \cdot \vec n =0\] erhält man \(\vec n\) als Lösung des LGS: \[\begin{align} a_1\cdot n_1 + a_2\cdot n_2 + a_3 \cdot n_3 =& \, 0\\ b_1\cdot n_1 + b_2\cdot n_2 + b_3 \cdot n_3 =& \, 0\\ \end{align}\]
Rechnen mit Vektoren
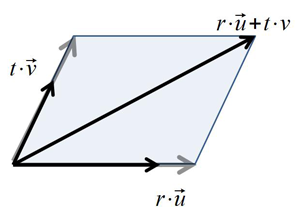
Mit Hilfe der Linearkombination \(t \cdot \vec v + r \cdot \vec u \) kann man jeden Vektor der Ebene, die von \( \vec u\) und \( \vec v\) aufgespannt wird darstellen.
Wie man sieht: die zwei Vektoren spannen ein Parallelogramm auf.
Wie man sieht: die zwei Vektoren spannen ein Parallelogramm auf.
Es gelten die folgenden Rechengesetze für Vektoren:
\(
\begin{eqnarray}
\hbox{Kommutativgesetz} &:& \vec{a} + \vec{b} &=& \vec{b} + \vec{a}\\
\hbox{Assoziativgesetz} &:& \vec{a} + (\vec{b} + \vec{c})&=& (\vec{a} + \vec{b}) + \vec{c}\\
\end{eqnarray}
\)
und mit \(r,s \in\mathbb{R}:\)
\(
\begin{eqnarray}
\hbox{Assoziativgesetz} &:& r\cdot(s \cdot \vec{a}) &=& (r \cdot s) \cdot \vec{a}\\
\hbox{Distributivgesetz} &:& r \cdot(\vec{a} + \vec{b})&=& r \cdot\vec{a} + r \cdot\vec{b} \\
\end{eqnarray}
\)
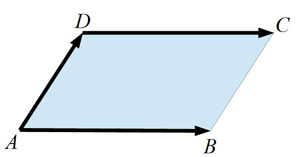Bekannt sind die Punkte \(A\), \( B\) und \(D \): gesucht ist der 4. Punkt, so dass das Viereck \(ABCD\) ein Parallelogramm ergibt. Wegen \(\vec{AB} = \vec{DC}\) gilt: \( \vec c = \vec d + \vec{AB} \)
Geraden im Raum
Eine Gleichung der Form \(g: \overrightarrow x = \overrightarrow p + t \cdot \overrightarrow u\) mit \( t\in\mathbb{R} \) beschreibt eine Gerade mit Stützvektor \(\overrightarrow p\) und Richtungsvektor \(\overrightarrow u \).
Die Zahl \(t \)nennt man Parameter.
Die Zahl \(t \)nennt man Parameter.
\(A\) liegt auf der Geraden, der Stützvektor kann also \(\overrightarrow a =\left( \begin{array}{c}1\\2 \\3 \end{array} \right)\) sein.
Der Richtungsvektor berechnet sich mit \(\overrightarrow{AB} = \left( \begin{array}{c} -1-1\\0-2 \\3-3 \end{array} \right).\)
Gesuchte Gleichung ist demnach \(g: \overrightarrow x = \left( \begin{array}{c}1\\2 \\3 \end{array} \right) + t \cdot \left( \begin{array}{c} -2\\-2 \\0 \end{array} \right).\)
Alternativ hätte man man auch \(\overrightarrow b\) als Stützvektor nehmen können. Oder statt \(\left( \begin{array}{c} -2\\-2 \\0 \end{array} \right)\) ein "Vielfaches" hiervon, z.B.: \(\left( \begin{array}{c} 1\\1 \\0 \end{array} \right)\).
Liegt der Punkt \(P(-1|0|3)\) auf der Geraden \(g: \overrightarrow x = \left( \begin{array}{c}1\\2 \\3 \end{array} \right) + t \cdot \left( \begin{array}{c} -2\\-2 \\0 \end{array} \right).\)?
Lösung: Man löst die Gleichung:\(\left( \begin{array}{c} -1\\0 \\3 \end{array} \right) = \left( \begin{array}{c}1\\2 \\3 \end{array} \right) + t \cdot \left( \begin{array}{c} -2\\-2 \\0 \end{array} \right).\), bzw. man überprüft, ob die 3 Gleichungen \(\begin{eqnarray} -1 &=& 1 -2t \\ 0 &=& 2-2 t \\ 3 &=& 3\\ \end{eqnarray} \) eine gemeinsame Lösung haben.
Hier sieht man, das wegen der gemeinsamen Lösung \(t=1\) gilt: \(P\in g\).
Lösung: Man löst die Gleichung:\(\left( \begin{array}{c} -1\\0 \\3 \end{array} \right) = \left( \begin{array}{c}1\\2 \\3 \end{array} \right) + t \cdot \left( \begin{array}{c} -2\\-2 \\0 \end{array} \right).\), bzw. man überprüft, ob die 3 Gleichungen \(\begin{eqnarray} -1 &=& 1 -2t \\ 0 &=& 2-2 t \\ 3 &=& 3\\ \end{eqnarray} \) eine gemeinsame Lösung haben.
Hier sieht man, das wegen der gemeinsamen Lösung \(t=1\) gilt: \(P\in g\).
Bei einer Raute sind alle 4 Seiten gleich lang. Die Diagonalen \(e \) und \(f \) schneiden sich orthogonal. es gilt:
$$ A = \frac{1}{2} e\cdot f.$$
Außerdem kann man den Flächeninhalt auch über das Kreuzprodukt \( F = | \vec a \times \vec b | \)berechnen, wobei \( \vec a\) und \( \vec b\), die Seiten der Raute sind.
| zueinander parallel | Richtungsvektoren sind linear abhängig \( \vec u = k \cdot \vec v\) und \(P\) liegt nicht in \(h\) (Punktprobe negativ) | |
| identisch | Richtungsvektoren sind linear abhängig und \(P\) liegt in \(h\) (Punktprobe positiv) | |
| sich schneidend | die Gleichung \( \vec p + r \cdot \vec u = \vec q + s \cdot \vec v \) hat eine Lösung | |
| zueinander windschief | die Gleichung \( \vec p + r \cdot \vec u = \vec q + s \cdot \vec v \) hat keine Lösung |
\(x_1\)-Achse: \(g: \overrightarrow x = t \cdot \left( \begin{array}{c} 1\\0 \\0 \end{array} \right).\)
\(x_2\)-Achse: \(g: \overrightarrow x = t \cdot \left( \begin{array}{c} 0\\1 \\0 \end{array} \right).\)
\(x_3\)-Achse: \(g: \overrightarrow x = t \cdot \left( \begin{array}{c} 0\\0 \\1 \end{array} \right).\)
\(x_2\)-Achse: \(g: \overrightarrow x = t \cdot \left( \begin{array}{c} 0\\1 \\0 \end{array} \right).\)
\(x_3\)-Achse: \(g: \overrightarrow x = t \cdot \left( \begin{array}{c} 0\\0 \\1 \end{array} \right).\)
Gegenseitige Lage im Raum
$$\tilde a \cdot x_1 +\tilde b \cdot x_2 + \tilde c \cdot x_3 = d$$
bzw., wenn man die Gleichung durch \(d\) teilt.
$$ a \cdot x_1 + b \cdot x_2 + c\cdot x_3 = 1$$
In diese Gleichung kann man die Koordinaten der Spurpunkte einsetzen und man erhält:
$$ {1 \over 3} \cdot x_1 + {1 \over 4} \cdot x_2 + {1 \over 6}\cdot x_3 = 1.$$
Diese Gleichung wird mit dem kleinsten gemeinsamen Vielfachen (kgV. hier 12) durchmultilipziert und man hat die Ebenengleichung.
$$E \colon 4 \cdot x_1 + 3 \cdot x_2 + 2\cdot x_3 = 12.$$
Zwei Geraden \( g: \vec x = \vec p + t\cdot\vec u \) bzw. \( h: \vec x = \vec q + r\cdot\vec v \) können entweder:
- sich schneiden (es gibt einen gemeinsamen Punkt),
- windschief sein (es gibt keinen gemeinsamen Punkt).
- parallel sein, falls \( \vec u \sim \vec v \) und \(\vec p \notin h\) Punktprobe negativ
- identisch sein, falls \( \vec u \sim \vec v \) und \(\vec p \in h\) Punktprobe positiv
Gegeben ist eine Gerade \( g: \vec x = \vec p + t\cdot\vec u \) und eine Ebene \( E: ax_1 + bx_2 + cx_3 = d\) mit Normalenvektor \(\vec n = \left( \begin{array}{c} a\\b \\c \end{array} \right)\).
Folgendes ist möglich:
- \(\vec u \cdot\vec n \neq 0 \): Die Gerade schneidet die Ebene.
- \(\vec u \cdot\vec n = 0 \) und \(p\notin E\): Die Gerade ist parallel zur Ebene und g liegt nicht in E.
- \(\vec u \cdot\vec n = 0 \) und \(p\in E\): Die Gerade ist parallel zur Ebene und g liegt in E.
Gegeben sind zwei Ebenen \( E_1: a_1x_1 + b_1x_2 + c_1x_3 = d_1\) bzw. \( E_2: a_2x_1 + b_2x_2 + c_2x_3 = d_2\). Man untersucht, ob die zwei Normalenvektoren \(\vec n_1\) bzw. \(\vec n_2\) Vielfaches voneinander sind.
Folgendes ist möglich:
- \(\vec n_1 \neq k\cdot\vec n_2\): Die Ebenen schneiden sich in einer Geraden,
- \(\vec n_1 = k\cdot\vec n_2\) und die Koordinatengleichungen sind nicht equivalent : Die Ebenen sind parallel,
- \(\vec n_1 = k\cdot\vec n_2\) und die Koordinatengleichungen sind equivalent : Die Ebenen sind identisch.
Ebenen im Raum
Eine Gleichung der Form \(E: \overrightarrow x = \overrightarrow p + t \cdot \overrightarrow u + s \cdot \overrightarrow v\) mit \( t, s \in\mathbb{R} \) beschreibt eine Ebene mit Stützvektor \(\overrightarrow p\) und Spannvektoren \(\overrightarrow u, \overrightarrow v \).
Die Zahlen \(t, s \) nennt man Parameter.
Die Vektoren \(\overrightarrow u \neq 0\) und \( \overrightarrow v \neq 0 \) dürfen keine Vielfachen voneinander sein.
Die Zahlen \(t, s \) nennt man Parameter.
Die Vektoren \(\overrightarrow u \neq 0\) und \( \overrightarrow v \neq 0 \) dürfen keine Vielfachen voneinander sein.
Stelle eine Gleichung einer Ebene durch die 3 Punkte \(A(1|2|0)\), \(B(3|0|4)\) und \(C(0|5|6)\) auf.
Liegen die 3 Punkte nicht auf einer Geraden, so kann man eine Ebene aufstellen, die die 3 Punkte enthält. Man wählt einen der drei Ortsvektoren als Stützvektor und berechnet dann die 2 Spannvektoren:
Stützvektor: \( \overrightarrow p = \left( \begin{array}{c} 1\\2 \\0 \end{array} \right) \) und die Spannvektoren
Liegen die 3 Punkte nicht auf einer Geraden, so kann man eine Ebene aufstellen, die die 3 Punkte enthält. Man wählt einen der drei Ortsvektoren als Stützvektor und berechnet dann die 2 Spannvektoren:
Stützvektor: \( \overrightarrow p = \left( \begin{array}{c} 1\\2 \\0 \end{array} \right) \) und die Spannvektoren
- \( \overrightarrow{AC}= \left( \begin{array}{c}0-1\\5-2 \\6-0 \end{array} \right) = \left( \begin{array}{c}-1\\3 \\6 \end{array} \right)\)
- \( \overrightarrow{AB}= \left( \begin{array}{c}3-1\\0-2 \\4-0 \end{array} \right)= \left( \begin{array}{c}2\\-2 \\4 \end{array} \right)\)
Liegt der Punkt \(P(1|2|3)\) auf der Ebene \(E\) \( \vec x = \left( \begin{array}{c} 1\\2 \\0 \end{array} \right)
+ t \cdot \left( \begin{array}{c}-1\\3 \\6 \end{array} \right)
+ s \cdot \left( \begin{array}{c}2\\-2 \\4 \end{array} \right)
\) ?
Man berechnet das LGS: \(\begin{eqnarray} 1 &=& 1 &-&t &+& 2s \\ 2 &=& 2 &+&3t &-&2s \\ 3 &=& 0 &+&6t &+&4s \\ \end{eqnarray} \)
Hat das LGS eine Lösung, so liegt der Punkt in der Ebene, gibt es keine Lösung, so liegt der Punkt nicht auf \(E\).
Besser wäre es, wenn die Ebenengleichung in Koordinatenform gegeben wäre, so wäre die Rechnung einfacher.
Man berechnet das LGS: \(\begin{eqnarray} 1 &=& 1 &-&t &+& 2s \\ 2 &=& 2 &+&3t &-&2s \\ 3 &=& 0 &+&6t &+&4s \\ \end{eqnarray} \)
Hat das LGS eine Lösung, so liegt der Punkt in der Ebene, gibt es keine Lösung, so liegt der Punkt nicht auf \(E\).
Besser wäre es, wenn die Ebenengleichung in Koordinatenform gegeben wäre, so wäre die Rechnung einfacher.
Schnitt einer Ebene mit den Koordinatenachsen ergeben die Spurpunkte. Es kann maximal 3 und mindestens 1 Spurpunkt geben.
Schnitt einer Ebene mit den Koordinatenebenen ergeben die Spurgeraden.
Schnitt einer Ebene mit den Koordinatenebenen ergeben die Spurgeraden.
- Die Parameterdarstellung aus dem Stützvektor \(\vec p \) und den zwei Spannvektoren \( \vec u\) bzw. \(\vec v\). $$ E: \overrightarrow x = \left( \begin{array}{c} p_1\\p_2 \\p_3 \end{array} \right) + t \cdot \left( \begin{array}{c} u_1\\u_2 \\u_3 \end{array} \right) + s \cdot \left( \begin{array}{c} v_1\\v_2 \\v_3 \end{array} \right) $$
- Die Koordinatenform
\(E: n_1 \cdot x_1 + n_2 \cdot x_2 + n_3 \cdot x_3 = d\), wobei \(\vec n = \left(\begin{array}{c} n_1\\n_2 \\n_3 \end{array}\right) = \left(\begin{array}{c} u_1\\u_2 \\u_3 \end{array}\right) \times \left(\begin{array}{c} v_1\\v_2 \\v_3 \end{array}\right) \) der Normalenvektor der Ebene ist. - Die Normalengleichung \(E: (\vec x -\vec p)\cdot \vec n =0. \)
- Hat man 3 Punkte, so stellt man zunächst die Parameterform auf.
- mit Hilfe des Kreuzproduktes erhält man aus den Spanvektoren den Normalenvektor
- Mit Hilfe des Normalenvektors und einem Punkt (aus dem Stützvektor) erhält man die Koordinatengleichung und die Normalengleichung.
- aus der Koordinatengleichung erhält man die Parmetergleichung, indem man ein LGS löst.
Eine mögliche Ebenengleichgung ist
$$
{ 1 \over 4}\cdot x_1 + { 1 \over 5}\cdot x_2 + { 1 \over 6}\cdot x_3 = 1 .
$$
Multipliziert man diese Gleichung mit dem Hauptnenner (hier 60) durch, so erhält man \(15 x_1 + 12 x_2 + 10 x_3 = 60. \)
\(x_1x_2\) - Ebene: \(x_3 =0\)
\(x_1x_3\) - Ebene: \(x_2 =0\)
\(x_2x_3\) - Ebene: \(x_1 =0\)
\(x_1x_3\) - Ebene: \(x_2 =0\)
\(x_2x_3\) - Ebene: \(x_1 =0\)
Es gilt:
\(ax_1 + bx_2 + cx_3 = d \) Man darf \(d=1\) setzen. Setzt man nacheinander die Punkte \(S_1\) , \(S_2\) und \(S_3\) ein, so erhält man:
\(\frac{1}{3}x_1 + \frac{1}{4}x_2 + \frac{1}{5}x_3 = 1\).
Mit 60 multiplizieren (das kleinste gemeinsame Vielfache der Nenner:
\(20 x_1 + 15 x_2 + 12x_3 = 60\).
Mit 60 multiplizieren (das kleinste gemeinsame Vielfache der Nenner:
\(20 x_1 + 15 x_2 + 12x_3 = 60\).
Abstände
Man berechnet die Hesse' sche Normalenform (HNF) $$E:\frac{ax_1 + bx_2 + cx_3 -d}{\sqrt{a^2 + b^2 +c^2}}=0.$$ Dann gibt für den Abstand \(d\) des Punktes \(R(r_1|r_2|r_3)\) zu \(E\):
$$ d(R;E)= \left| \frac{ar_1 + br_2 + cr_3 -d}{\sqrt{a^2 + b^2 +c^2}} \right|$$
Man stellt eine Lotfußgerade \(l\) von \(R\) orthogonal zu \(E\) auf:
$$ l: \vec x = \vec r + t \cdot \vec n_E.$$ Diese schneidet man mit \(E\) und erhält so den Lotfußpunkt \(L\). Der Betrag des Vektors \(\vec {RL}\) entspricht dem gesuchtem Abstand.
Man stellt eine Hilfsebene \(H\) auf, die \(R\) enthält und orthogonal zur Geraden \(g: \vec x = \vec p + t\cdot \vec v\) ist.
$$ H: (\vec x - \vec r)\cdot \vec{v}=0 $$
Diese schneidet man mit der Geraden und erhält so den Lotfußpunkt \(L\). Der gesuchte Abstand entspricht dann dem Betrag des Vektors \(\vec{RL}\).
Die Geraden $$ g: \vec x = \vec p + s\cdot \vec u \hbox{ und } h: \vec x = \vec q + t\cdot \vec v $$ sollen windschief zueinander sein.
Man stellt eine Hilfsebene $$H : \vec x =\vec p + s\cdot \vec u + t\cdot \vec v $$ auf, diese ist parallel zu \(h\) und enthält die Gerade \(g\). Mit Hilfe des Kreuzproduktes \(\vec n = \vec u \times \vec v\) kann man die Ebene auch in Koordinatenform aufstellen.
Das Problem hat sich dann auf die Berechnung des Abstandes Punkt \(Q\) zur Ebene \(H\) reduziert:
$$d(g;h)= \left| (\vec p - \vec q)\cdot \vec {n_0}\right|.$$
Skalarprodukt
Das Skalarprodukt von zwei Vektoren \(\overrightarrow a = \left( \begin{array}{c}a_1\\a_2 \\a_3 \end{array} \right) \) und \(\overrightarrow b = \left( \begin{array}{c}b_1\\b_2 \\b_3 \end{array} \right)\) ist definiert durch:
\[\overrightarrow a \cdot \overrightarrow b = a_1 \cdot b_1 + a_2 \cdot b_2 + a_3 \cdot b_3.\] Zwei Vektoren sind genau dann orthogonal, falls das Skalarprodukt 0 ist:
$$\overrightarrow a \perp \overrightarrow b \Longleftrightarrow a_1 \cdot b_1 + a_2 \cdot b_2 + a_3 \cdot b_3 = 0. $$
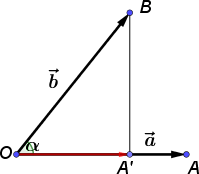Für den Ortsvektor \(\vec{m}\) gilt:
\(
\begin{eqnarray}
\vec a \cdot \vec b &=& \vec a \cdot (\vec{OA'}+\vec{A'B})\\
&=& \vec a \cdot \vec{OA'}+\vec a\cdot\vec{A'B}) \\
&=& \vec a \cdot \vec{OA'}+0 \\
&=& |\vec a|\cdot\vec a_0 \cdot |\vec{OA'}|\cdot \vec a_0 \\
&=& |\vec a| \cdot |\vec{OA'}|\cdot \vec a_0\cdot\vec a_0 \\
&=& |\vec a| \cdot |\vec{OA'}|.
\end{eqnarray}
\)
Außerdem gilt im rechtwinkligen Dreieck \(\Delta OA'B \): \(\cos(\alpha)=\frac{|\vec{OA'}|}{|\vec b|} \), so erhält man $$\vec a \cdot \vec b = |\vec a|\cdot |\vec b| \cdot \cos(\alpha), {\rm\; für \; } 0^\circ \leq \alpha\leq 180^\circ $$
Zwei Geraden \(g\) und \(h\)haben die Richtungsvektoren \(\vec u\) und \(\vec v\) und zwei Ebenen \(E\) und \(F\) for Normalenvektoren \(\vec n_E\) bzw. \(\vec n_F\). So gilt für die Schnittwinkel:
- Gerade / Gerade: \( \displaystyle\cos(\alpha ) = \frac{|\vec u \cdot \vec v |}{|\vec u|\cdot |\vec v|}, \; 0^\circ \leq \alpha \leq 90^\circ\)
- Ebene / Ebene: \(\displaystyle\cos(\alpha ) = \frac{|\vec n_E \cdot \vec n_F |}{|\vec n_E|\cdot |\vec n_F|}, \; 0^\circ \leq \alpha \leq 90^\circ\)
- Ebene / Gerade : \(\displaystyle\sin(\alpha ) = \frac{|\vec u \cdot \vec n_E |}{|\vec u|\cdot |\vec n_E|}, \; 0^\circ \leq \alpha \leq 90^\circ\)
Vektorprodukt
Vektorprodukt: die Vektoren \(\vec a\) und \(\vec b\) spannen eine Ebene auf, \( \vec c = \vec a \times \vec b \) steht senkrecht auf dieser Ebene.
\[\begin{align}
\vec c =&\, \vec a \times \vec b \\
=& \left(\begin{array}{}a_x\\a_y\\a_z\end{array}\right) \times \left(\begin{array}{}b_x\\b_y\\b_z\end{array}\right) \\
\left(\begin{array}{}c_x\\c_y\\c_z\end{array}\right) =& \left(\begin{array}{}a_x\\a_y\\a_z\end{array}\right) \times \left(\begin{array}{}b_x\\b_y\\b_z\end{array}\right) \\
\end{align}\]
- Flächeninhalt eines Paralellogramms, welches von zwei Vektoren \(\vec a\) und \(\vec b\) aufgespannt wird: $$A=\left| \vec a \times \vec b \right|$$
- Volumen eines Spates, welches von drei Vektoren \(\vec a, \vec b\) und \(\vec c\) aufgespannt wird: $$V=\left|\vec c \cdot\left( \vec a \times \vec b\right) \right|$$